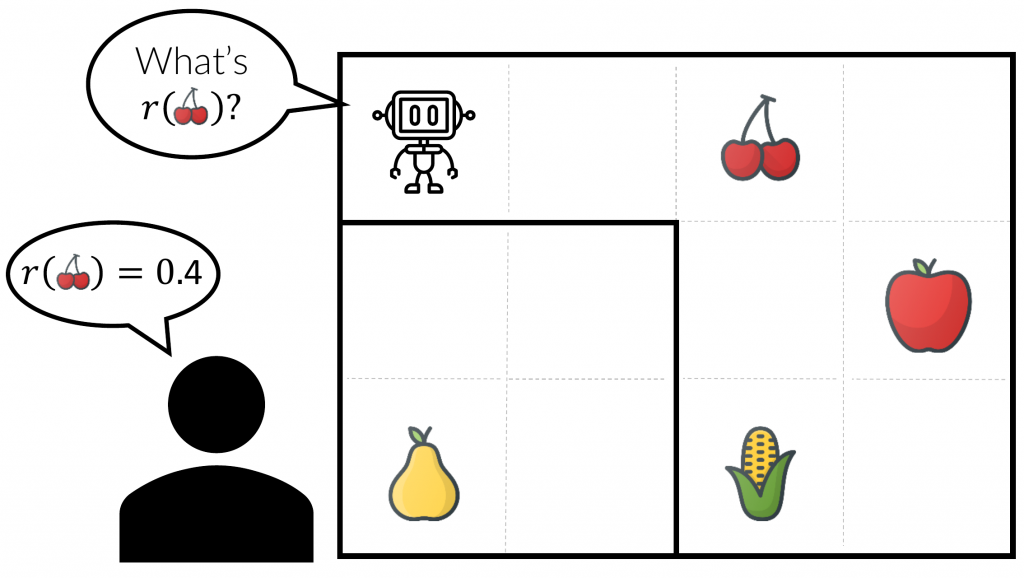
Figure 1: The robot needs to learn the user’s food preferences to decide what to collect. We propose a method that can significantly reduce the number of queries necessary by focusing on queries that are informative about which policy is optimal.
Recently, reinforcement learning (RL) has shown impressive performance on tasks with a well-specified reward function, such as Atari games. Unfortunately, a reward function is often not available in the real world. Say you want to train an RL agent to drive a car. What is a good reward function for driving? Often researchers hand-craft complicated reward functions for such tasks, but this is cumbersome and prone to error. More generally, misspecified rewards can lead to unintended and unsafe behavior due to specification gaming.
A promising alternative is to learn a model of the reward from human feedback. By, for example, asking humans to compare trajectories and judge which one solves a task better, we can learn a reward function for tasks that are difficult for humans to specify manually.[1]For example, see Sadigh et al. 2017 or Christiano et al. 2017. But, this approach can require a lot of human feedback. For example, in work by OpenAI, a human evaluator had to answer 900 comparison queries to teach a simulated agent to do a backflip.
To scale this approach to more complex tasks, we need to reduce the number of queries a human evaluator has to answer. One way to do this is to aim to select the most informative queries to make using active learning.
What are the most informative queries?
Different criteria are commonly used in active learning to select which queries to make. Often, these aim at reducing the uncertainty about the function we want to learn — in this case, the reward function. However, in RL, we don’t care directly about approximating the reward function, but instead, we want to use the reward model to learn a good policy. Consequently, we don’t really need to reduce the uncertainty about the reward function everywhere. For example, some regions of the state space might not be relevant for finding the optimal policy because they are hard to reach, or we have already determined them to be suboptimal.
As an illustration of this, consider the gridworld environment in Figure 1. Here, the robot wants to collect food for a human, but it doesn’t know their preferences. Also, the robot can only walk four timesteps, so it has to decide which of the food to collect. The robot can ask the human about a specific item, and the human responds with the numerical value of that item. How many queries does the robot have to make to find the optimal policy in this environment?
Our first guess might be that the robot needs to make four queries and ask the human about each item in the environment to figure out the best strategy for collecting the human’s favorite food. However, it turns out the robot can do significantly better if it uses the fact that it doesn’t need to know the reward everywhere.
To see that, consider: without knowing anything about the value of the different items, which policies could be optimal? It turns out there are only two plausibly optimal policies: collecting the cherry and the corn, or collecting the cherry and the apple. No optimal policy will collect the pear because it is not reachable from the robot’s initial position (there is a wall in the way). All optimal policies will collect the cherry because it is on the way to collecting the corn or the apple.[2]Let’s assume that collecting more food is always better.
Hence, the robot only needs to ask two questions to find the optimal policy, one about the value of the corn and one about the value of the apple. In this simple example, it can find the optimal policy with half the number of queries about the reward.
Information directed reward learning
So, can we do something similar in more general environments? In our recent NeurIPS 2021 paper, we propose an approach we call Information Directed Reward Learning (or short “IDRL”) that does exactly this. The key idea is to formalize what we just saw in the gridworld example.
Intuitively, IDRL makes queries that help distinguish between plausibly optimal policies, which directly helps determine the best policy. Hence, IDRL is more aligned with the goal of RL than methods that uniformly reduce uncertainty on the state space,[3]For example, Bıyık et al. 2019 select queries that maximize the information gain about the whole reward function. and it is more general than other previous methods that only work for specific query types.[4]For example, Wilde et al. 2020 propose a method limited to pairwise comparisons of trajectories.
More specifically, IDRL considers two plausibly optimal policies that the current model is uncertain about; let’s call them \pi_1 and \pi_2. It then aims to select queries that are most informative about how to distinguish these two policies, which we formalize as maximizing the information gain about the difference in expected return between \pi_1 and \pi_2. Formally, the IDRL criterion for selecting queries is:
where q is a query the agent can make, \hat{y} is the expected response, \hat{G} is the agent’s current belief about the expected return of a policy, and \mathcal{D} is the data collected so far. This acquisition function formalizes selecting queries that are informative about finding the optimal policy, and it is not specific to the form of the queries q, which is a problem with some of the prior work.
Note that IDRL captures the intuition we built before in the gridworld example. In that example, G(\pi_1) = r(\text{cherry}) + r(\text{corn}) and G(\pi_2) = r(\text{cherry}) + r(\text{apple}). Therefore G(\pi_1) - G(\pi_2) = r(\text{corn}) - r(\text{apple}), and therefore the information gain will be maximized for querying either the corn or the apple.
To implement IDRL, we have to make a few more design choices: which model to use for the reward function? How to determine plausibly optimal policies? And how to find a policy for a given reward function? In our paper, we propose two different implementations of IDRL: one uses Gaussian process (GP) models, and one uses deep neural networks (DNNs). We can compute the IDRL objective exactly and efficiently for GP models, whereas, for DNNs, we have to approximate it. In both cases, we determine the plausibly optimal policies using Thompson sampling, which allows us to translate the agent’s belief about the reward into a belief about which policies are optimal. For more technical details, see the full paper.
Experiments in MuJoCo
In our paper, we test this approach on a series of environments and compare it to alternative active learning methods. The results generally demonstrate that using IDRL can be much more sample efficient than active learning methods that uniformly reduce the uncertainty about the reward, especially if we ultimately care about finding a good policy.
For example, in one experiment, we train an agent to find a goal in a simple maze in the MuJoCo simulator. The agent can ask about short clips of behavior, and it gets noisy observations of the sum of rewards over these clips.[5]The feedback is simulated using an underlying true reward function that the agent cannot access.
In the following plot, we evaluate the agent’s regret, a measure of how much worse the agent is than the optimal policy (the best value is 0), as a function of the number of times it queried about the reward:
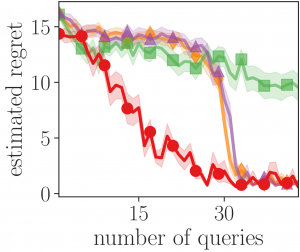
This plot shows that IDRL (
) needs much fewer queries to learn a good policy than alternative methods, such as maximizing information gain about the reward[6]Bıyık et al. 2019 (
), Expected Improvement[7]A common choice of acquisition function in Bayesian optimization. (
), or uniform sampling (
). IDRL is more sample efficient because it targets queries to regions that are important for finding the optimal policy. In this maze, the agent has to move in the right direction and then stop at the goal. Regions that are past the goal are less important, and consequently, IDRL queries them less, whereas the other methods query everywhere similarly often to reduce uncertainty everywhere.
Outlook
IDRL is a promising approach to improve the sample efficiency of reward learning methods for reinforcement learning. But there are a couple of conceptual and practical limitations that we hope to address in future work.
So far, our work focuses on improving the sample efficiency in terms of queries about the reward to humans. In this project, we assumed interactions with the environment to be cheap, which is usually not the case in practice. Much work in RL aims to improve the sample efficiency in terms of environment interactions. For practical applications, it would be necessary also to consider this dimension for IDRL.
IDRL is also not ideal for learning reward models that can be transferred between environments, because it aims to learn a good policy in a single environment. For example, if we remove the inner walls in the gridworld above during test time, the agent would not know if it should collect the pear or not. To improve the transferability of reward functions, future versions of IDRL could select queries that are informative about good policies in a distribution over environments instead of a single one. By choosing this distribution, a user could then manage the tradeoff between sample efficiency and transferability of the learned reward model.
Overall, IDRL promises to be a valuable addition to the set of existing active reward learning algorithms for situations in which it is crucial to reduce the amount of human feedback necessary.
This post is based on the following paper:
2021 | |
| |
Footnotes
| ↑1 | For example, see Sadigh et al. 2017 or Christiano et al. 2017. |
|---|---|
| ↑2 | Let’s assume that collecting more food is always better. |
| ↑3 | For example, Bıyık et al. 2019 select queries that maximize the information gain about the whole reward function. |
| ↑4 | For example, Wilde et al. 2020 propose a method limited to pairwise comparisons of trajectories. |
| ↑5 | The feedback is simulated using an underlying true reward function that the agent cannot access. |
| ↑6 | Bıyık et al. 2019 |
| ↑7 | A common choice of acquisition function in Bayesian optimization. |