Student Projects in LAS Group
We offer Semester Projects, Bachelor’s and Master’s theses in our group. Depending on your preference, there are opportunities for working on theory, methods, and applications. M.Sc. projects at LAS often result in publications at leading conferences.A list of topics for which we are actively recruiting students is given below. If you don’t see a project below that fits well, but you are interested in the kind of research our lab does, feel free to still reach out. To learn more about the research done in the group, visit our recent publications. You can also learn more about research by individual group members.
If you are interested in working with us, you can send an application by clicking the button below. Make sure that your email includes: a résumé, a recent transcript of records, your intended start date, and we highly recommend that you mention the projects you are interested in, members of the group with whom you would like to work, or recent publications by the group relevant to your interests.
If you are a bachelors or masters student but not a student at ETH, please see the opportunity listed in Applications for Summer Research Fellowships.
Current Topics
The detailed project proposals can be downloaded only from the ETH domain.Projects on LLM Safety and Alignment
Resources
People
Keywords: Large Language Models Safety, Reward Hacking, AI Control, Scalable Oversight
TriMoEmotion: Emotion-Rich Body Gestures Generation from Multi-Modal Data
Resources
People
- Manish Prajapat
- Hao Ma

Keywords: Large Language Models, Speech, Visual processing
Bridging the Gap: Enabling Soft Actor-Critic for High-Performance Legged Locomotion
Resources
People

Keywords: Legged locomotion, Soft Actor-Critic, Reinforcement learning, Sim-to-real transfer
Improving and Evaluating LLM Alignment
Resources
People
Keywords: Large Language Models, LLM Alignment, LLM Evaluation, Preference Learning
Sequential Confidence Estimation via Likelihood Mixing
Resources
People
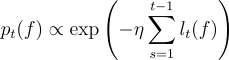
Keywords: online convex optimization, confidence sets, frequentist and Bayesian statistics, PAC-Bayes
Improving the Ability of Large Language Models
We offer various topics aimed at improving LLMs’ reasoning abilities.Resources
People
- Jonas Hübotter
- Ido Hakimi
Keywords: Large Language Models, Active Learning, Meta Learning, Computational Efficiency
General Areas
We offer projects in several general areas.- Probabilistic Approaches (Gaussian processes, Bayesian Deep Learning)
- Discrete Optimization in ML
- Online learning
- Large-Scale Machine Learning
- Causality
- Active Learning
- Bayesian Optimization
- Reinforcement Learning
- Meta Learning
- Learning Theory
Examples of Previous Master Theses
Transductive Active Learning: Theory and Applications
Awarded ETH Medal. Jonas Hübotter with Bhavya-Sukhija, Lenart Treven, and Yarden As. NeurIPS 2024. [paper]
Lifelong Bandit Optimization: No Prior and No Regret
Awarded ETH Medal. Felix Schur with Jonas Rothfuss and Parnian Kassraie. UAI 2023. [paper]
BaCaDI: Bayesian Causal Discovery with Unknown Interventions
Alex Hägele with Jonas Rothfuss and Lars Lorch. AISTATS 2023. [paper]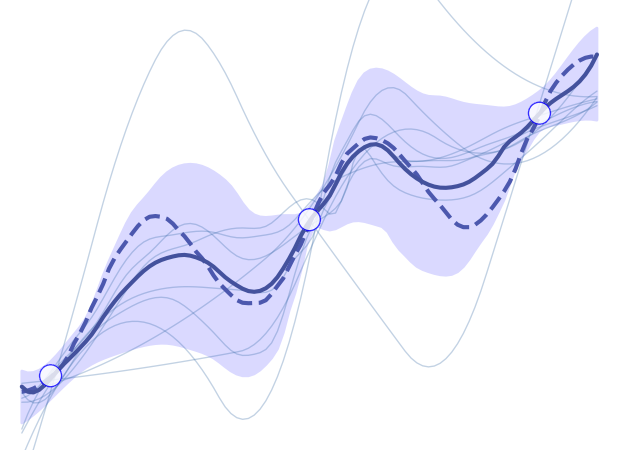
MARS: Meta-Learning as Score Matching in the Function Space
Kruno Lehman with Jonas Rothfuss. ICLR 2023. [paper]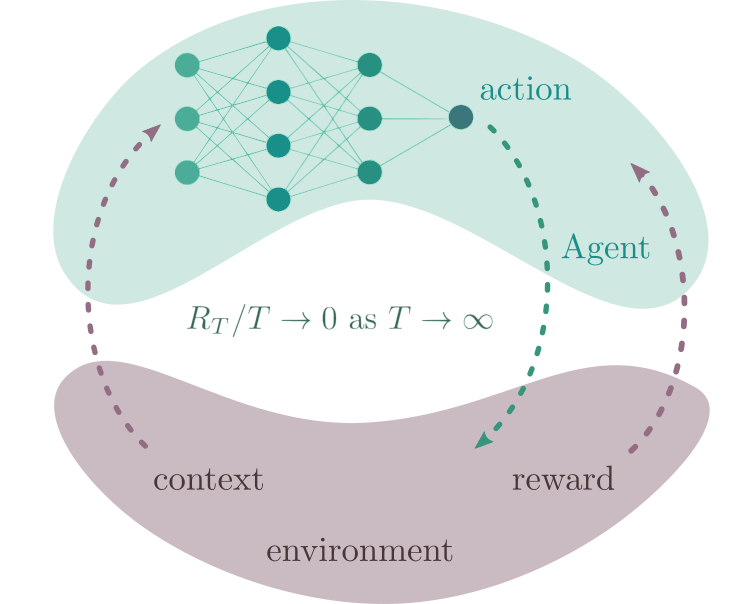
Neural Contextual Bandits without Regret
Parnian Kassraie with Andreas Krause. AISTATS 2022. [paper]
Near-Optimal Multi-Perturbation Experimental Design for Causal Structure Learning
Scott Sussex with Andreas Krause and Caroline Uhler. NeurIPS 2021. [paper] [blog]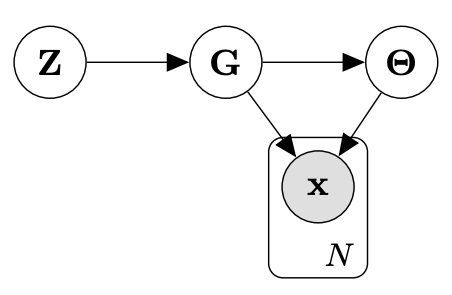
DiBS: Differentiable Bayesian Structure Learning
Awarded ETH Medal. Lars Lorch with Jonas Rothfuss. NeurIPS 2021. [paper] [blog]
PopSkipJump: Decision-Based Attack for Probabilistic Classifiers
Noman Ahmed Sheikh with Carl-Johann Simon-Gabriel. ICML 2021. [paper]Icons on this page are by www.flaticon.com.

